Redundant Connection

冗余的连接; LeetCode 684; LintCode 1088

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

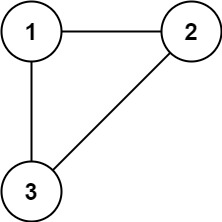
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

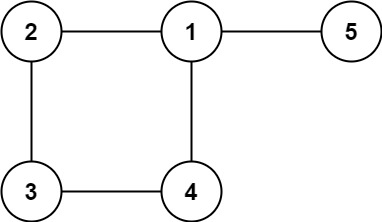
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

• n == edges.length

• 3 <= n <= 1000

• edges[i].length == 2

• 1 <= ai < bi <= edges.length

• ai != bi

• There are no repeated edges.

• The given graph is connected.

----------------------------------------------------------------------------

这题有官方solution。思路是:

从一张空白的图开始

从edges里面依次取出每一条edge,用[u,v]来表示:
   if u，v 在当前的图中连通:
      [u,v]就是答案 -> return [u,v]
   else:
      把edge [u,v]加入图中

这个套路很巧妙，之前没有碰到过。大概就是说，如果u,v本来就是连通的（在加入这条edge之前），那么这条edge就是多余的。

根据这个思路，有dfs和union find两种做法。我的code在下面。然后后面还有我自己的第三种的做法

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        #按照官方Solution 1的思路
        graph = collections.defaultdict(list)
        
        def dfs(current, target, visited):
            if current == target:
                return True
            if current in visited:
                return False
            visited.add(current)
            for n in graph[current]:
                if dfs(n, target, visited):
                    return True
            return False
        
        for u, v in edges:
            if dfs(u, v, set()):
                return [u,v]
            graph[u].append(v)
            graph[v].append(u)
            
        return []

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        #按照官方Solution 2的思路,利用 union find
        N = max(map(max, edges))
        father = [i for i in range(N+1)]
        
        def find(x):
            if father[x] != x:
                father[x] = find(father[x])
            return father[x]
        
        def union(x, y):
            father[find(x)] = find(y)
            
        for u, v in edges:
            if find(u) == find(v):
                return [u, v]
            else:
                union(u, v)
                
        return []

----------------------------

下面是我没看solution前写出来的做法。思路就是dfs来找环，找到环后，在这个环上找一条最后出现在edges中的边来作为答案

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        #找环
        nbs = collections.defaultdict(list)
        for u,v in edges:
            nbs[u].append(v)
            nbs[v].append(u)
            
        def dfs_find_loop(cur, pre, path, visited):
            if cur in visited:
                index = path.index(cur)
                return path[index:]
            
            visited.add(cur)
            path.append(cur)
            
            for neighbor in nbs[cur]:
                if neighbor == pre:
                    continue  #不走回头路
                loop = dfs_find_loop(neighbor, cur, path, visited)
                if loop:
                    return loop
                
            visited.remove(cur)
            path.pop()
            
            return None #这条路上找不到环
        
        loop = dfs_find_loop(1,-1,[],set())
        loop_edges = set()
        for i in range(len(loop)):
            loop_edges.add((loop[i], loop[(i+1) % len(loop) ])) #最后一条边是连接最后一个元素到元素0，所以要mod
            
        for u,v in reversed(edges): #按照题目要求，返回最后出现的那个
            if (u,v) in loop_edges or (v,u) in loop_edges:
                return [u,v]
        
        return []